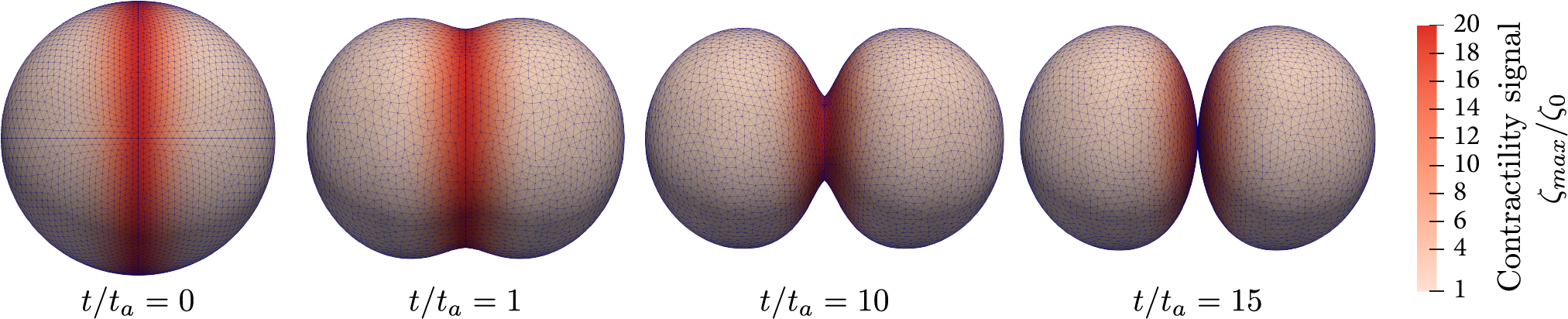A viscous active shell theory of the cell cortex - J. Mech. Phys. Solids

H. Borja da Rocha, J. Bleyer and H. Turlier*, Journal of the Mechanics and Physics of Solids 2022

Read more: publisher - preprint

The cell cortex is a thin layer beneath the plasma membrane that gives animal cells mechanical resistance and drives most of their shape changes, from migration, division to multicellular morphogenesis. Constantly stirred by molecular motors and under fast renewal, this material is well described by viscous and contractile active-gel theories. Here, we assume that the cortex is a thin viscous shell with non-negligible curvature and use asymptotic expansions to find the leading-order equations describing its shape dynamics, starting from constitutive equations for an incompressible viscous active gel. Reducing the three-dimensional equations leads to a Koiter-like shell theory, where both resistance to stretching and bending rates are present. Constitutive equations are completed by a kinematical equation describing the evolution of the cortex thickness with turnover. We show that tension and moment resultants depend not only on the shell deformation rate and motor activity but also on the active turnover of the material, which may also exert either contractile or extensile stress. Using the finite-element method, we implement our theory numerically to study two biological examples of drastic cell shape changes: cell division and osmotic shocks. Our work provides a numerical implementation of thin active viscous layers and a generic theoretical framework to develop shell theories for slender active biological structures.

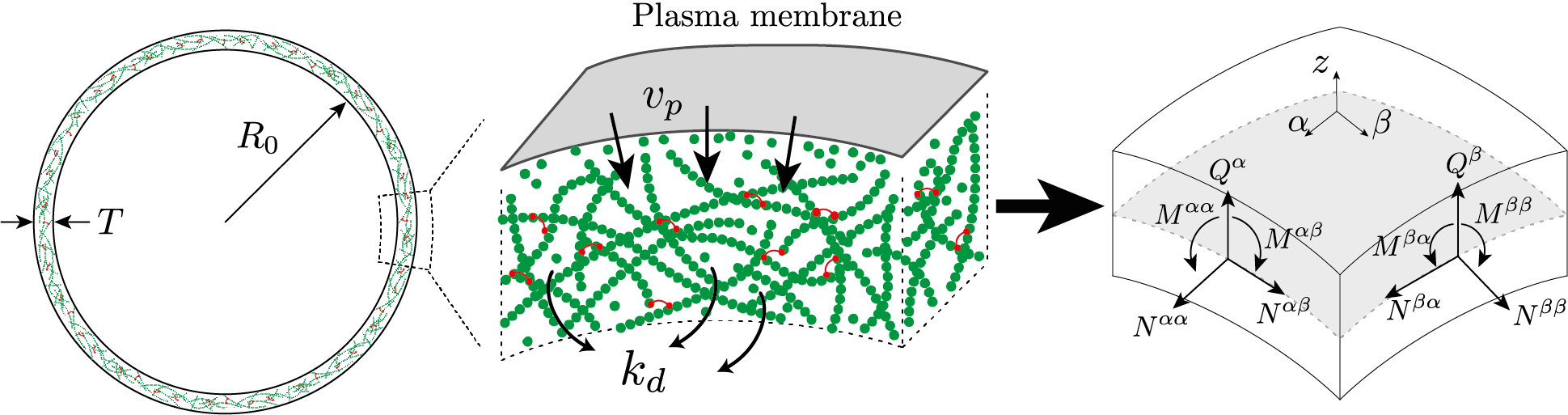
Schematic representation of the cell cortex, composed of actin filaments and actin-binding proteins, in particular myosin molecular motors. The cortex forms a thin layer of thickness 𝑇 ≪ 𝑅0 beneath the plasma membrane. The dimensional reduction into a thin shell theory consists in finding the two-dimensional approximate in-plane and transverse shear stress 𝑁𝛼𝛽 and 𝑄𝛼, and torque 𝑀𝛼𝛽 resultants, defined on the middle-surface of the shell.

Dynamic shape changes of a cell during cell division (cytokinesis) illustrated by successive timepoints of furrow constriction. Arrows represent the direction of the velocity field 𝒖.

Shape dynamics of a cell subjected to a hyperosmotic shock. In the left is the imposed volume variation over time.